В пятницу, 7 августа, состоялось открытие художественного проекта WebWeb, в котором я принимал участие. Не спрашивайте меня, что это все означает, я и сам не понимаю; это такое высокое искусство. Для меня самым интересным разделом был Death: если подвигать курсором влево-вправо, то можно увидеть, как по лошади ползет тень, описывая ее контуры.

В этом посте я расскажу, как сделать еще один плагин к jQuery как создавалась техническая часть этой страницы.
Макет от дизайнера
Дизайнер прислал мне макет, в котором он нарисовал 33 состояния тени.
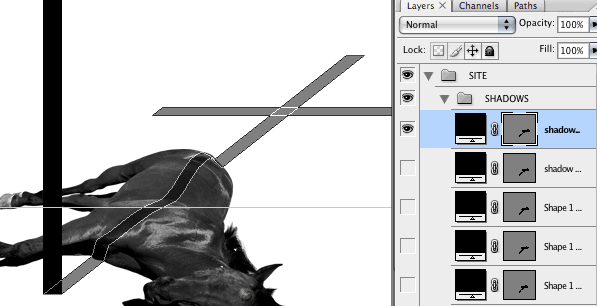
В принципе, его устраивало, чтобы тень менялась дискретно, то есть можно было просто показывать 33 картинки в зависимости от позиции курсора и не париться. Но меня этот вариант не нравится, так как в нем явно не хватало секса. Поэтому было решено сделать плавное перемещение тени.
Смотрим внимательно на саму тень. По сути, это две пересеченные линии, одна из них — перекладина — простая, как пять копеек, а вторую можно представить как обычную кривую, отрисованную контуром (stroke). Решение этой задачи будет выглядеть следующим образом: создаем кривые, которые описывают каждое состояние тени…

…а затем будем рассчитывать между координатами точек новую линию, в зависимости от позиции курсора.
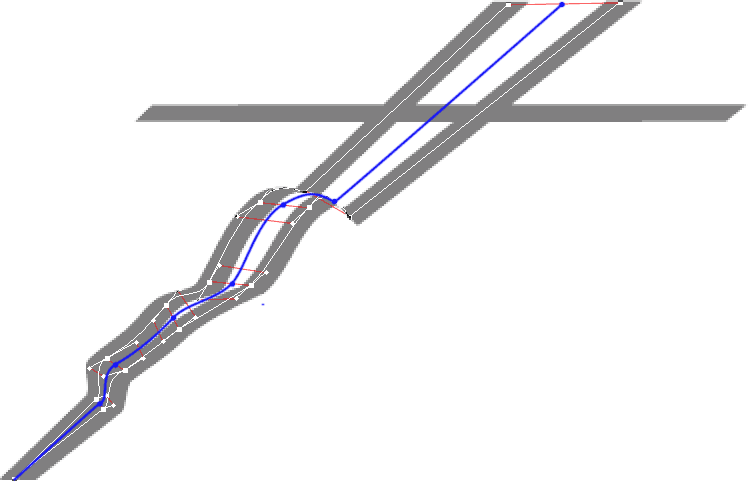
Важно помнить, что набор точек должен быть одним и тем же (то есть в одной линии не может быть больше или меньше точек, чем в другой). Я делал так: отрисовал первую тень, продублировал путь (path) и передвинул точки в другое положение. И так еще 31 раз.
Хранение кривых внутри JavaScript
Линии отрисовали, теперь нужно придумать, как будем их хранить и использовать в JS. У нас возможны два типа линий: обычная, прямая линия и кривая Безье. Сам контур тени представляет собой массив таких линий. Для удобства и краткости записи создаются две прокси-функции, которые просто будут возвращать объект с координатами:
/**
* Точка
*/
function p(x, y) {
return {x: x, y: y};
}
/**
* Кривая Безье
*/
function bz(cp1x, cp1y, cp2x, cp2y, x, y) {
return {
cp1x: cp1x,
cp1y: cp1y,
cp2x: cp2x,
cp2y: cp2y,
x: x,
y: y
};
}
// пример использования
var line = [p(381, 289), p(427.33, 254), bz(427, 254, 427, 244, 433, 237)];
Отлично, с форматом разобрались. Но есть один нюанс: помимо координат контура нужно хранить и угол наклона линии, чтобы можно было рассчитывать новую, динамическую линию между двумя заданными. Поэтому создаем еще одну прокси-функцию, которая будет создавать объект линии по заданным координатам.
var shadow = {
min: Number.POSITIVE_INFINITY,
max: Number.NEGATIVE_INFINITY,
lines: {},
degs: []
};
/**
* Добавляет линию, описывающую тень
* @param Массив точек
*/
function addLine() {
// преобразуем объект аргументов в настоящий массив
var points = Array.prototype.slice.call(arguments, 0);
/** Первая точка линии */
var first = points[0],
/** Последняя точка линии */
last = points[points.length - 1];
// считаем угол наклона линии
var deg = -Math.atan2(last.y - first.y, last.x - first.x) / Math.PI * 180;
shadow.degs.push(deg);
shadow.lines[deg] = points;
if (deg < shadow.min)
shadow.min = deg;
if (deg > shadow.max)
shadow.max = deg;
}
Как видите, я использую массив углов линий shadow.degs и хэш самих линий shadow.lines, где ключом является угол наклона. Все это нужно для того, чтобы быстро находить две соседние линии. Дополнительно я считаю минимальный и максимальный угол чтобы знать, в каких пределах производить расчеты.
Экспорт данных из фотошопа
На первый взгяд, это самая рутинная и скучная часть работы: все 33 контура тени теперь нужно перенести из фотошопа в JS, причем в том формате, который мы выбрали. Решение «в лоб» — наводить курсор на каждую точку кривой, запомнить координаты и записать их в JS. Потратил час только на то, чтобы таким образом записать 3–4 линии (и те с ошибками). Так дело не пойдет, нужно как-то автоматизировать этот процесс.
Я помню, что в адобовском иллюстраторе есть опция экспорта кривых в SVG, а у фотошопа есть функция экспорта кривых в иллюстратор (File → Export → Paths to Illustrator). Что ж, это уже что-то. Так как иллюстратора у меня нет, экспортированный файл высылаю дизайнеру и прошу его пересохранить в SVG.
Но все равно SVG не самый удобный формат для моей задачи. Во-первых, у его Path Data есть два типа данных — абсолютные и относительные координаты. Например, запись l10,20 означает смещение на 10 пикселей по горизонтали и 20 пикселей по вертикали относительно предыдущей точки, а запись L10,20 уже означает смещение в координату x=10, y=20. Во-вторых, в SVG присутствует короткая запись однотипных инструкций: например, L10,20 L30,40 L0,60 можно записать как L10,20,30,40,0,60 и иллюстратор любит этим пользоваться. В общем, парсинг из SVG далеко не тривиальная задача.
Оказывается, формат .ai вполне себе текстовый. Более того, координаты кривых там записываются в двольно простом формате и это именно то, что мне нужно.
... %Adobe_Photoshop_Path_Begin:<< /defaultFill false >> *u %AI3_Note:<< /operation /xor /defaultFill false >> 1 XR 551.5000 248.5000 m 596.0000 283.5000 L 601.0000 285.5000 595.5000 299.5000 607.0000 303.0000 C 616.0000 309.0000 626.0000 317.5000 634.0000 323.5000 c 642.0000 329.5000 662.5000 339.0000 670.0000 345.5000 c 677.5000 352.0000 690.5000 376.5000 699.0000 384.5000 C 711.0000 398.5000 719.0000 379.5000 y 854.5000 487.0000 l N *U %Adobe_Photoshop_Path_End ...
Пишем простенький парсер, которые преобразует набор координат в наш формат (кому интересно, вот он) и уже через полчаса у меня появился набор всех контуров.
Вспомнить школу
Настало время приступить к программированию самой логики. Алгоритм работы будет следующим: во время движения мышки рассчитываем угол наклона линии, соединяющей курсор и начальную точку (в нашем случае это столб), добавляем к этому углу 180˚ и получаем угол наклона тени. Затем находим два статических контура, между которыми находится полученный угол, строим новый контур и отрисовываем его. Все просто, не так ли? 🙂
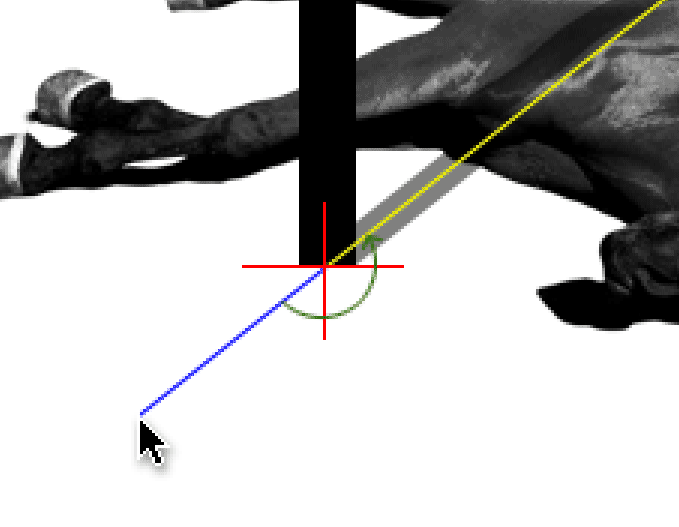
Прежде, чем начать, нам нужно вспомнить школьный курс математики и геометрии. У большинства моих преподавателей было типичное совковое мировоззрение: задавая вопрос «зачем мне все это нужно?» я получал ответ вроде «это нужно для поступления в ВУЗ», а о способе применения этих знаний в жизни тактично умалчивали. Если б я знал, что буду заниматься программированием анимации и графики, я бы совсем иначе относился к учебе. Так что если вы еще учитесь — наматывайте на ус и не повторяйте моих ошибок 🙂
Первое, с чем нужно освоится, это координатное пространство. В компьютерной графике оно не такое, как преподают в школе, из-за этого я до сих пор с непривычки не могу вести нормальные расчеты на бумаге:
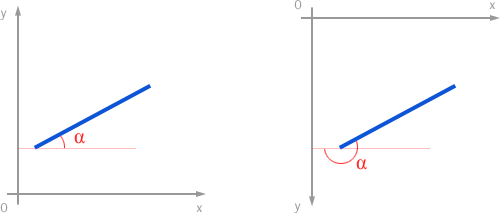
Как видите, одна и та же линия и ее угол наклона рассчитывается по-разному в декартовой и компьютерной системе координат.
При движении мышки мы знаем ее X и Y координаты, соответственно, можем рассчитать и угол наклона линии, соединяющей курсор и начальную точку, через арктангенс. Затем просто переводим этот угол в другую систему координат с помощью поворота (не претендую на изящность решения, так как всю геометрию и алгебру забыл):
// считаем угол наклона линии от курсора до начальной точки var cursor_deg = Math.atan2(y, x) + Math.PI / 4 * 3; // считаем угол линии контура тени var line_deg = 315 - cursor_deg / Math.PI * 180;
Следует помнить, что все вычисления с углами через Math.xxx функции должны вестись в радианах, а не углах.
Итак, нужный угол мы получили, теперь осталось на основе него построить контур тени. Как указано выше, алгоритм следующий: находим два статических контура, между которыми располагается искомый контур, и считаем новый. Расчет ведется следующим образом: берется отрезок, соединяющий две одинаковые точки, и его длина умножается на некий коэффициент. Этот коэффициент рассчитывается исходя из близости искомого контура к одному из статических. Например, если искомый контур находится ровно посередине, то коэффициент будет 0.5, если ближе к первому, то, например 0.2 и так делее. На практике все довольно просто:
/**
* Высчитывает параметры контура для указанного угла
* @param {Number} deg
* @return {Array}
*/
function calculateLine(deg) {
// угол должен быть не меньше минимального и не больше максимального
deg = Math.min(shadow.max, Math.max(shadow.min, deg));
var result = [], d1, d2, coeff;
for (var i = 1; i < shadow.degs.length; i++) {
d1 = shadow.degs[i - 1];
d2 = shadow.degs[i];
if (deg >= d1 && deg <= d2) {
// нашли нужный диапазон, считаем коэффициент
coeff = 1 - (deg - d1) / (d2 - d1);
break;
}
}
if (coeff !== null) {
var l1 = shadow.lines[d1],
l2 = shadow.lines[d2];
// считаем координаты нового контура
for (var j = 0; j < l1.length; j++) {
var p1 = l1[j],
p2 = l2[j],
point = {};
for (var p in p1) if (p1.hasOwnProperty(p)) {
point[p] = p2[p] + (p1[p] - p2[p]) * coeff;
}
result.push(point);
}
}
return result;
}
Начинаем рисовать
Основные элементы логики описаны, осталось собрать их вместе. Для рисования я буду использовать Canvas, для IE, соответственно, VML с помощью прослойки excanvas. Пишем промежуточный класс CanvasAdapter, который будет рисовать графику по выбранному ранее формату записи контуров, пишем вспомогательные функции, отслеживающие перемещение курсора и изменения размера экрана (чтобы не тратить лишний раз ресурсы на расчет координат начальной точки контуров) и проверяем:

Вполне неплохо. Обращаем внимание на то, что контур тени — так как это обычная кривая — неестественно смотрится на ягодицах лошади:
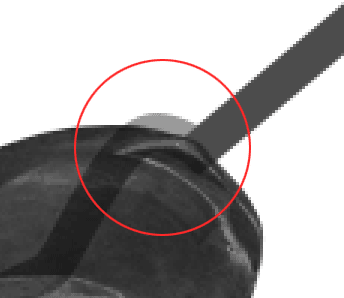
Нужно отрезать выступающий кусок контура. Для решения этой задачи на потребуется создать конструкцию из трех слоев. Первый слой — рисуем прямую линию от начала и до конца тени, как будто лошади вообще нет и у нас голый пол. Второй слой — сама лошадь в PNG, она будет скрывать ту часть прямой тени, которая находится под лошадью. И, наконец, третий слой — полноценный контур тени, на который наложена маска. То есть получается два canvas-элемента, между которыми располагается картинка.
Помним, что у нас есть замечательный конвертер, который может из ai-формата сделать наш внутренний формат, поэтому в фотошопе быстренько рисуем маску и экспортируем ее в JS. Особая точность маске не нужна, у меня она получилась вот такой:

Собираем все вместе, смотрим:

Осталось совсем немного: отрезать верхушку тени, чтобы она смотрелась естественно. Можно воспользоваться методом canvas.clearRect(), однако в IE, из-за ограниченной поддержки excanvas, это не сработает. Поэтому размещаем сверху <div> с белым фоном, который будет скрывать ненужную часть. Просто и эффективно.
Рисуем перекладину
Последняя часть марлезонского балета — нарисовать перекладину. Она представляет из себя обычный прямоугольник, который должен правильно искажаться в зависимости от рассчитанного угла наклона тени. Решаем задачу следующим образом: находим пересечение текущего контура тени (достаточно прямой линии, кривые Безье не нужны) и горизонтальной линии перекладины, искажаем текущее координатное пространство матричным преобразованием и рисуем прямоугольник:
var intersection = lineIntersection(0, line_y, 1000, line_y, last_point.x, last_point.y, first_point.x, first_point.y); canvas.transform(1, 0, (line_deg - 90) / 50, 1, intersection.x - 125, intersection.y); canvas.fillRect(0, 0, 250, 10);
Вот и все. Делаем окончательный тюнинг, чтобы все работало гладко и смотрим на окончательный результат. Осталось добавить, что excanvas не поддерживает и маски, поэтому тень в IE смотрится не очень красиво, но для проекта это не критично. Интересующиеся могут исследовать исходный код страницы, чтобы увидеть все детали и жуткий баг Оперы, связанный с использованием масок в canvas.
